|
|
EBSD und BKD |
|
|
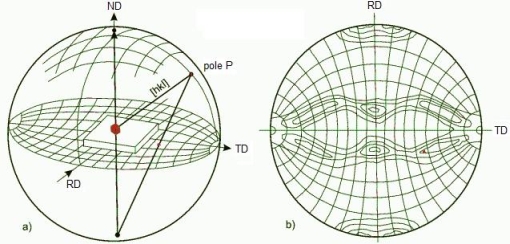
Texturanalyse Ursprünglich wurde die Textur nur qualitativ durch Interpretation von Polfiguren analysiert, die in den meisten Fällen röntgenographisch gemessen wurden. Eine umfassende Darstellung der Anfangsperiode bis 1962 findet sich in der Monographie "Texturen metallischer Werkstoffe" von G. Wassermann und J. Grewen [1]. Eine Polfigur Phkl gibt die Menge oder den Volumenanteil dV/V der Kristallite an, deren kristallographische Richtungen <hkl> in bestimmte Richtungen (α, β) im Raum weisen: dV/V= Phkl(α, β) sinα dαdβ (1) Die Referenzrichtungen im Raum werden in der Regel entsprechend der Symmetrie der Probe, des Herstellungsprozesses oder des Einsatzzwecks gewählt. Beispielsweise wählt man im Fall von Walzblechen die Blechnormalenrichtung (NR, ND) und die Walzrichtung (WR, RD). Graphisch wird die Häufigkeits- oder die Dichteverteilung in den Raumrichtungen (α, β) auf der 3D Lagenkugel angegeben, die Lagekugel wird aus praktischen Gründen meistens stereographisch in die 2D "Äquator"-Ebene projiziert und „(normale) Polfigur“ genannt, Abb. 1.
Eine einzelne Polfigur gibt für alle Kristallite die Lagen der kristallographischen Richtungen <h k l> an. Dabei kann jeder Kristallit beliebig um diese Richtung gedreht sein, ohne dass das die Polfigur ändert. Zur Beschreibung der vollständigen Orientierung eines Kristalls werden drei Orientierungswinkel gebraucht. Hierzu können die Orientierungswinkel (α, β) einer herausgegriffenen Kristallrichtung <hkl> sowie ein Drehwinkel γ um diese Richtung herum benutzt werden. Aus mehreren Gründen ist es jedoch zweckmäßig, anstelle dieser drei Winkel die drei sogenannten Eulerwinkel (φ1, Φ, φ2) zu verwenden, welche die Drehung des Kristallkoordinatensystems in das Referenzsystem der Probe angeben. Diese Winkel liegen der Orientierungsdichtefunktion, ODF, zugrunde.
Die Quantitative Texturanalyse [2] Die ODF gibt die Menge oder denVolumenanteil der Kristallite in der Orientierung (φ1, Φ, φ2) an [3, 4]
Der multiplikative Faktor, der bei der Dichtefunktion f(g) = f (φ1, Φ, φ2) steht, berücksichtigt mit Φ die Größe des Volumenelements im
Orientierungsraum und mit 1/8π2
die Normierung der Texturfunktion auf
Die Die „iterative Positivitätsmethode“ [5] ist ein Reihenentwicklungsverfahren, das in vielen Fällen die Unbestimmbarkeit der ungeraden Koeffizienten überwindet und somit die vollständige Funktion f(g) Gl. (3) liefert: Auch Polfiguren sind Dichtefunktionen, so dass sie - wie die ODF - nur positive Werte aufweisen dürfen. In den gemessenen Polfiguren werden also zunächst die nicht gemessenen Bereiche auf 0 (oder einen (willkürlichen) positiven Wert) gesetzt. Daraus wird nach der Reihenentwicklungsmethode eine ODF berechnet und aus dieser wiederum neue Polfiguren. Im nächsten Iterationsschritt werden die gemessenen Bereiche dieser Polfiguren mit den Messwerten aufgefüllt, während negative Werte auf 0 gesetzt werden, usw. Die Reihenentwicklungsmethode mit Iteration und Positivitätsbedingung ermöglicht bereits nach wenigen Iterationsschritten eine besonders kompakte mathematische Beschreibung der Textur. Mit Kenntnis von wenigen C-Koeffizienten können unmittelbar (anisotrope) Tensoreigenschaften des Vielkristalls ausgedrückt werden. Bei kubischer Probensymmetrie, wie sie zum Beispiel in gewalzten Stählen vorliegt, genügen bei der Berechnung von r-Werten und von Fließortkurven die Koeffizienten niedriger Ordnung (bis l = 4). Für die Berechnung der Texturtransformation sind auch die Koeffizienten höherer Ordnung der vollständigen ODF von Bedeutung. An dieser Stelle muss hervorgehoben werden, dass nicht nur das Vorhandensein und die Stärke gewisser Vorzugsorientierungen für die Beurteilung der Textur wesentlich sind, sondern auch das Fehlen oder die Unterrepräsentanz von Texturkomponenten im Vergleich zu einer regellosen Orientierungsverteilung. Wenn beispielsweise Körner mit Orientierungen im Gefüge fehlen, deren Gleitsysteme günstig zu einer äußeren Beanspruchungsrichtung liegen, so kann die plastische Verformung erheblich behindert sein. Ebenso werden Rekristallisation und Gefügeausbildung bei einer Glühbehandlung durch das Fehlen bestimmter Orientierungen im Ausgangsmaterial beeinflusst. Es genügt also in der Regel nicht, die Stärke einiger weniger Vorzugsorientierungen als Charakteristikum der Textur anzugeben. Abgesehen davon kann die Angabe von Volumenanteilen für die identifizierten Texturkomponenten an der Gesamttextur selbst für dieselbe Probe irreführend sein, wenn die Modellfunktionen in alternativen Inversionsverfahren (z.B. Kugeln, Rotationsellipsoide im Orientierungsraum) nicht an die tatsächlich vorliegenden Formen der einzelnen Komponenten angepasst werden. Die Angabe eines Texturindex als Verhältnis der Intensitäten von Beugungsinterferenzen aus einem θ − 2θ-Scan kann stark fehlerbehaftet sein. Ein Vorteil der Reihenentwicklungsmethode besteht darin, dass keine speziellen Modellfunktionen für Vorzugsorientierungen verwendet werden und dennoch eine effiziente quantitative Beschreibung, sowohl der Maxima als auch der Minima, der vollständigen Orientierungsdichteverteilung in Form der C-Koeffizienten erzielt wird. Graphisch wird dies durch die Darstellung der (berechneten) Polfiguren und der ODF mittels Linien gleicher Belegungsdichte erreicht, die auf Vielfache der regellosen Orientierungsverteilung normiert werden. Zweckmäßig ist dabei die explizite Markierung des Niveaus, das der regellosen Textur entspricht. Die Messung von Polfiguren Die Messungvon Polfiguren erfolgt meistens mit Hilfe eines Texturgoniometers in Bragg-Brentano-Geometrie [6]. Das Texturgoniometer ermöglicht es, den Bragg‘schen Winkel θ einzustellen und damit den beugenden Netzebenentyp {hkl} zu wählen, sowie die Probe durch die gesamte Lagenkugel zu drehen, so dass alle Richtungen (α, β) der Probe in Reflexionsstellung gebracht werden können. (Die Kippwinkel χ und Drehwinkel δ des Goniometers werden in Polarwinkel umgerechnet.)
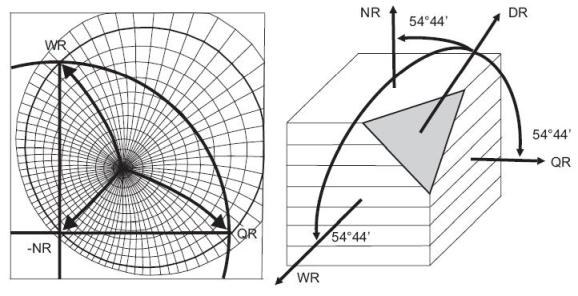
1. Die Rückstrahlmethode In Rückstreuung an planen Proben gemessenen Polfiguren nimmt die Genauigkeit wegen der Defokussierung der Bragg-Brentano-Geometrie [6] mit zunehmender Probenkippung ab. Für Kippwinkel c > 70° kommen noch Abschattungen oder mechanische Begrenzungen des Kippbereichs hinzu, so dass der äußere Rand der Polfigur nicht erfasst werden kann. Die Rückstrahlmethode liefert sogenannte „unvollständige Polfiguren“ im Winkelbereich 0° ≤ α ≤ 70°. 2. Die Transmissionsmethode Auch in Durchstrahlung kann die Lagenkugel nicht vollständig gemessen werden, da es aus apparativen Gründen ebenfalls zu Abschattungen kommt. Für große Kippwinkel wird die Absorptionskorrektur unsicher, denn die effektive Probendicke nimmt extrem zu. Man erhält röntgenographisch sowohl in Rückstreuung als auch in Durchstrahlung nur unvollständige Polfiguren mit nicht gemessenen Bereichen am Rand bzw. im Zentrum. Über die nicht erfassten Bereiche liegen zunächst keine Texturinformationen vor. Die Normierung der Belegungsdichten auf 1 bezüglich der vollen Lagenkugel kann daher nicht vorgenommen werden. Dieser Nachteil kann rechnerisch ausgeglichen werden, wenn aus mehreren Polfiguren die Orientierungsdichtefunktion berechnet wird. 3. Die röntgenographische Messung vollständiger Polfiguren VollständigePolfiguren, welche die gesamte Lagenkugel abdecken, können nach einer zum Teil sehr aufwändigen Probenpräparation röntgenographisch gemessen werden. Um sie in einem einzigen Messvorgang zu erhalten liegt es nahe, aus der Probe eine kleine Kugel, im Durchmesser von 100 - 500 μm entsprechend der Breite des Primärstrahls, herauszutrennen. Sie muss bei der Messung vollständig in den primären Röntgenstrahl eintauchen. Durch Drehung um zwei Achsen kann dann die Lagenkugel vollständig abgetastet werden. Da sich die Absorption bei einer kugelförmigen Probe nicht mit den Drehwinkeln ändert, braucht keine weitere Korrektur vorgenommen zu werden. Die Normierung der Belegungsdichte auf 1 für die gesamte Lagenkugel genügt. Die Herstellung von sehr kleinen kugelförmigen Proben ist jedoch schwierig und problematisch, weil bei der Präparation die Textur verändert werden könnte oder die kleine Probe nicht repräsentativ für das Werkstück ist. Kann, wie gut angenähert bei Walzblechen, eine orthorhombische Probensymmetrie vorausgesetzt werden, so genügt es, nur einen Quadranten der Polfigur zu messen. Handelt es sich zudem um ein kubisch kristallines Material, so können spezielle Probenpräparationen angewandt werden, die über das Blechvolumen integrieren: Die erste Möglichkeit besteht in der Herstellung einer würfelförmigen Probe und Messung der (unvollständigen) Polfiguren in Reflexion nacheinander auf drei zueinander senkrecht stehenden Seitenflächen. Diese können dann zu einer vollständigen Polfigur zusammengesetzt werden. Eine über das Blechvolumen integrierende Polfigurmessung am Längs- oder Querschliff statt parallel zur Blechebene ist jedoch nur bedingt möglich, weil die Blechdicke selten zu ausreichend großen Messflächen führt. Messtechnisch weniger aufwändig ist die Schrägschnittmethode, nur wird jetzt an einer Fläche gemessen, die senkrecht zur Richtung α0 = 54,74°, β0 = 45° steht [7]. Das ist die Raumdiagonale des aus Walzrichtung, Querrichtung und Normalrichtung gebildeten Würfels. Die in Reflexion aufgenommene röntgenographische Polfigur mit Kippwinkeln α von 0° bis 65° deckt bereits praktisch einen ganzen Quadranten in der stereographischen Projektion ab, Abb. 3. Für diese Kippwinkel ist in Reflexion die Absorptionskorrektur nicht unbedingt erforderlich. Da bei Blechen die vier Quadranten symmetrisch gleichwertig sind, liefert die Schrägschnittmethode somit vollständige Polfiguren. Weil die Messung jetzt an einer schräg liegenden Fläche erfolgt, ist noch eine Koordinatentransformation erforderlich, die die Resultate in die Bezugsebene, die Blechebene, zurücktransformiert. Diese Fläche enthält den gesamten Blechquerschnitt und ist also repräsentativ für das gesamte Blechvolumen. Ihre Ergebnisse stimmen wesentlich besser mit r-Wert-Messungen am gesamten Blech überein.
Die Größe der so angeschnittenenFläche im Blech ist jedoch meistens für die Messung noch zu klein. Deshalb werden mehrere Bleche übereinandergestapelt, so dass eine Kompositprobe entsteht, an der dann die genannte Fläche angeschnitten wird. Zunächst werden quadratische Abschnitte des Blechs zu einem Würfel seitenrichtig so aufeinandergestapelt und verklebt, dass die Walzrichtung und Blechnormale der Blechstücke parallel zueinander verlaufen. Dann wird eine Ecke des Würfels zu einer Fläche abgeschrägt, so dass die Flächennormale in der Würfeldiagonalen liegt und zuden Achsen NR, WR und QR des Blechs den Winkel von 54°44' bildet. Früher wurden auch sich ergänzende Rückstreu- und Durchstrahlungspolfiguren von möglichst derselben Probenstelle kombiniert, so dass sie sich zu vollständigen Polfiguren überlagern ließen. Die Anpassung der Intensitäten ist schwierig, da der Überlappungsbereich relativ schmal und die Normierung der Belegungsdichten nicht möglich ist. Die Erzeugung vollständiger Polfiguren ist heute nicht mehr erforderlich. Bereits aus wenigen unvollständigen, experimentellen Polfiguren kann die dreidimensionale Orientierungs-Dichte-Funktion (ODF) zum Beispiel mit der iterativen Reihenentwicklungsmethode berechnet werden. Aus ihr lassen sich beliebige, auch nicht messbare Bereiche und vollständige Polfiguren mit hoher Genauigkeit berechnen. 4. Die Polfigurmessung mit Synchrotron- undNeutronenstrahlen Texturuntersuchungen können in ganz ähnlicher Weise wie mit
Röntgenstrahlen auch mit Neutronenstrahlen oder harter Synchrotronstrahlung
durchgeführt werden. Die Messprinzipien stimmen weitgehend überein. An den
meisten Forschungsreaktoren stehen Beamlines mit Vierkreisdiffraktometern für
Einkristall-Untersuchungen zur Verfügung. Diese sind praktisch identisch mit
Texturgoniometern. Es ist lediglich ein anderes Steuerprogramm erforderlich. Allerdings
sind Verfügbarkeit und Messzeit an Teilchenbeschleunigern und
Forschungsreaktoren der Großforschungsanlagen sehr begrenzt. Ein Vorteil der Neutronenbeugung [8] und der Beugung mitharter Synchrotronstrahlung gegenüber der Röntgenstrahlung liegt in der
wesentlich größeren Eindringtiefe. Sie ist für Eisen in der Größenordnung von
einigen Zentimetern verglichen mit etwa einigen 10 µm für Röntgenstrahlen.
Daraus resultieren spezifische Vorteile: 5. Inhomogene Texturen Wegen der starken Absorption von Röntgenstrahlung in Materie kann in der Rückstrahlung nur eine dünne Oberflächenschicht der Probe (10 – 100 µm) untersucht werden. Die Textur in der Tiefe muss daher durch Abtragen von Oberflächenschichten ermittelt werden. Das ist insbesondere dann wichtig, wenn die Textur inhomogen ist, also von der Oberfläche zur Mitte hin variiert. Dies ist bei Walzblechen häufig der Fall. Die Untersuchung des gesamten Texturprofils in Schichten von der Oberfläche bis zur Blechmitte ist sehr aufwändig. Daher werden Untersuchungen mit der Rückstrahlmethode meistens auf die Blechmitte beschränkt. Das Blech wird dann von der Oberfläche her bis zur Blechmitte abgetragen. Die so erhaltene Textur ist die Blechmittentextur. Wenn die Textur mit dem r-Wert des gesamten Blechs verglichen werden soll, dann ist die Blechmittentextur nicht repräsentativ. Die Polfigurmessung mit Röntgen-, Synchrotron- und Neutronenstrahlen zielt auf integrale Bestimmung der gemittelten Textur in großen Probenvolumina ab. Lokale Inhomogenitäten im Mikrobereich werden wegen der begrenzten Ortsauflösung nicht erfasst. Für diese Untersuchungen sind ortsauflösende Sondenmethoden und insbesondere die Elektronenmikroskopie zuständig (TEM [9] und EBSD). 1 G. Wassermann und J. Grewen: Texturen metallischer Werkstoffe.
Springer Verlag, Berlin 1962 Energiedispersive Beugung mit der Röntgenrasterapparatur Die energiedispersive Röntgenbeugung (ED XRD) ist eine äußerst vielseitige Methode [1]. Aus der Verschiebung und der Verbreiterung der Beugungspeaks können lokale Gitterdehnungen mit guter Ortsauflösung ermittelt werden. Das Verfahren ist somit eine Grundlage für die Messung lokaler Eigenspannungen erster und zweiter Art. ED XRD ermöglicht die ortsaufgelöste Messung von Pofiguren [2] und Elementkonzentrationen (Mikro-Röntgen-Fluoreszenz-Analyse, Mikro-RFA). Die Funktion eines energiedispersiven Detektors entspricht einem ortsempfindlichen Detektor in der konventionellen Röntgenbeugung. Für die Energie von Beugungspeaks gilt nach der Bragg-Gleichung Ehkl = n h c/(2 dhkl sin ϑ). Dabei ist h die Plancksche Konstante und c die Lichtgeschwindigkeit, dhkl sind die Netzebenenabstände. Der Winkel 2θ zwischen dem "weißen" Primärstrahl und dem Blickwinkel des Detektors ist für alle Reflexe eine Konstante. Die Trennung der Peaks erfolgt energiedispersiv. Der Detektor misst die Intensität an einem so vorgegebenen Polfigurpunkt P(α, β) simultan für mehrere Netzebenen {hkl}, welche die Bragg-Bedingung erfüllen.
Nach erfolgreichen ersten Versuchen [3] wurde eine Röntgen-Rasterapparatur aufgebaut und zu einem leistungsfähigen automatischen Messsystem entwickelt, das speziell die Untersuchung der Verteilung der lokalen Textur in frei in Größe und Form definierbaren Probenbereichen ermöglicht [4]. Sie besteht aus einem kommerziellen Röntgengenerator und einer offenen rechnergesteuerten Eulerwiege mit x-y Probentisch (Philips X'Pert). Der energiedispersive Detektor, zum Beispiel ein Peltier-gekühlter Bruker X'Flash-Detektor, ist auf den 2θ-Kreis des Goniometers montiert.
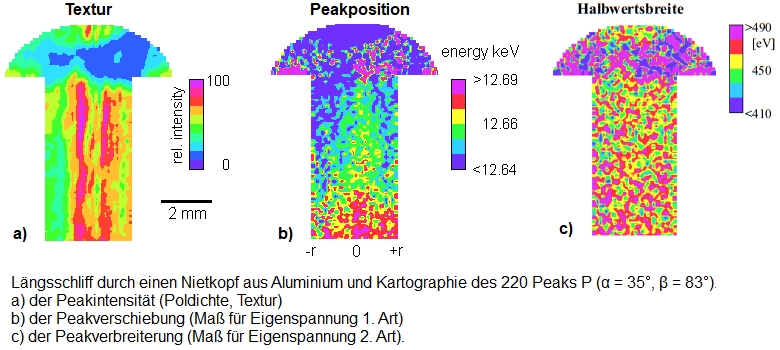
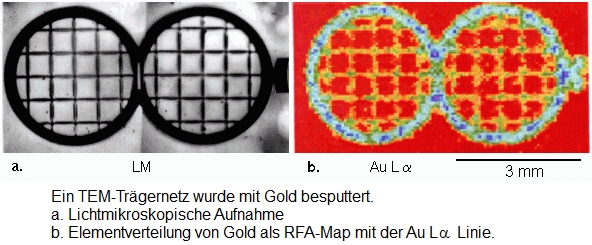
Für die Texturkartographie muss die globale Textur mit ihren Vorzugsorientierungen bereits im Voraus bekannt sein. Daher sind vor der eigentlichen Texturkartographie zunächst Polfigurmessungen und eine Texturanalyse mit Bestimmung der ODF (Orientierungsverteilungsfunktion) durchzuführen. Ein Umsetzen und Nachjustieren der Probe ist in dem hier entwickelten Kombinationsgerät nicht erforderlich. In der Regel werden die Polfiguren mit einer Ortsauflösung von etwa 0,2 bis 4 mm aufgenommen. Dadurch erhält man einen Überblick über die wichtigsten kristallographischen Vorzugsrichtungen bezogen auf einen ausgewählten Bereich der Probe. Einzelne interessierende Polfigurpunkte, die bestimmten Richtungen der Netzebenennormalen entsprechen, werden dann für die Texturkartographie ausgewählt. Meist sind dies signifikante Maxima in der Polfigur, die auf eine Vorzugsorientierung bestimmter Kristallite hinweisen. Entsprechend dieser Polfigurmaxima werden dann Dreh- und Kippwinkel der Probe in der Eulerwiege eingestellt. Die örtliche Verteilung dieser Poldichten wird durch eine Rastermessung aufgenommen (= Texturkartographie), indem die Probe bei feststehender Goniometereinstellung und unter der feststehenden Röntgensonde schrittweise verschoben wird. Die Schrittweite des frei definierbaren Probenmessrasters des rechnergesteuerten x-y Probentisches ist an den Durchmesser der Röntgensonde auf der Probenoberfläche angepasst. In der Dissertation von Armin Fischer [5] wird an einem breiten Spektrum von Beispielen gezeigt, dass Texturinhomogenitäten in nahezu allen Materialien auftreten, die einen Verformungs- oder Wärmebehandlungsprozess durchlaufen haben. Beispiele sind eine Münzprägung, Schlagbuchstaben in einem massiven Aluminiumblech, eine gratgewalzten Probe, ein gewalzter Titan-Nickel-Einkristall, eine Elektronenstrahl-Schweißnaht, eine Reibschweißnaht, ein warmstranggepresster und anschließend kaltgezogener Kupfer-Eisen-Verbundwerkstoff sowie eine Gesteinsfaltung in einer geologischen Hämatit-Probe. Für einen Aluminium-Niet wird neben der Texturverteilung auch die Verteilung der lokalen Gitterdehnungen mit guter Ortsauflösung gemessen und kartographiert. In Materialien, die mehrere Elemente enthalten, kann simultan zur Texturverteilung die Elementverteilung lokal bestimmt werden (Mikro-RFA). Die Ortsauflösung ist in allen Anwendungsfällen vom verwendeten Durchmesser der Primärstrahlblende abhängig und beträgt etwa 20 bis 100 µm. Noch kleinere Blendendurchmesser sind mit konventionellen Röntgen-Generatoren aus Intensitätsgründen nicht praktikabel. Eine Kapillaroptik im Primarstrahl kann bei kleinen Sonden zu einem wesentlichen Intensitätsgewinn führen. Allerdings wäre die Beschneidung des kontinuierlichen Primärstrahlspektrums durch die spektrale Filterwirkung ein Nachteil für ED XRD. Eine sehr hohe Ortsauflösung unter 0,1 µm wird in der energiedispersiven Beugung mit Synchroton-Strahlung erreicht. Ein großes Potential versprechen energiedispersive Multiarray-Detektoren. Synchotron-Apparaturen sind in der materialwissenschaftlichen Forschung zu einem enormen Beitrag in der Lage. Sie stehen aber weltweit nur einer Handvoll Wissenschaftlern zur Verfügung. Trotz der schnellen Weiterentwicklung elektronenmikroskopischer Texturmessverfahren können in einigen Anwendungen die Texturverteilungen nur mit einer Röntgenrasterapparatur untersucht und in Verteilungsbildern kartographiert werden. Beispiele sind stark verformte, sehr feinkörnige oder für die Elektronenmikroskopie ungeeignete Proben, wenn diese nicht vakuumfest sind oder durch den Elektronenbeschuss zerstört werden.
_______ [1] E. Laine und I. Lähteenmäki: The energy dispersive X-ray diffraction method: Annotated bibliography 1968-78. |
. Die Orientierungsdichtefunktion
f(g) kann nicht direkt gemessen werden, sondern wird durch eine „Polfigurinversion“
(vorzugsweise durch Koeffizientenvergleich mit der Reihenentwicklungsmethode) aus
den gemessenen Polfiguren berechnet. Die Polfiguren werden dazu durch
Kugelflächenfunktionen 
, die f(g) durch verallgemeinerte
Kugelfunktionen 
dargestellt:
sind
Koeffizienten, die die Textur charakterisieren. Diese Koeffizienten sind
wichtig, da auf ihnen Formeln zur Berechnung des r-Wertes und der Fließortkurve
beruhen. Eine ausführliche Darstellung der Berechnung der
Orientierungsverteilungsfunktion aus Polfiguren wurde in [3, 4] gegeben.
Bei der Polfigurmessung kann die
Kristallrichtung [hkl] nicht von der Gegenrichtung 
unterschieden
werden („Friedel’sche Regel“). Das hat zur Folge, dass in Gl. (3) nur die
Koeffizienten mit geraden Werten des Index l bestimmt werden können. Die
Koeffizienten mit ungeraden l-Werten sind auf diese Weise unbestimmbar. Man
weiß zunächst nur, dass sie nicht negativ sein können, denn die ODF ist eine
Dichtefunktion. Würde man sie in Gl. (3) ignorieren, so erhielte man eine
verfälschte Orientierungsdichtefunktion. Bei Werkstoffen mit kubischer
Kristallsymmetrie ist der dadurch entstehende Fehler in der Größenordnung von
10 bis 20% des Maximalwertes der Textur.
R.
Schwarzer: Röntgen-Rasterapparatur zur Aufnahme von
Textur-Verteilungsbildern mittels energiedispersiver Beugung. |
|