|
|
EBSD und BKD |
|
Orientierungsstereologie -
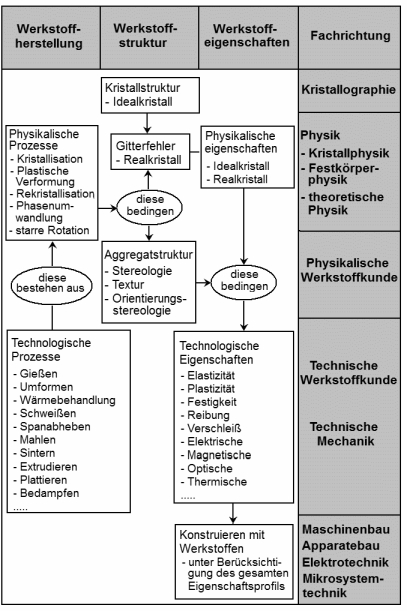
1. Was ist Orientierungsstereologie? Der größte Teil aller Feststoffe ist kristallin oder besitzt zumindest einen kristallinen Anteil. Das gilt für Werkstoffe – Metalle, Keramik, Polymere, genauso wie für geologische und biologische Naturstoffe – Erze und Gesteine, Knochen, Holz, Muscheln ... Die Liste ließe sich beliebig fortsetzen. Die Kristalle in diesen Stoffen sind zwar klein und haben nicht die schönen regelmäßigen Formen wie wir sie aus der Kristallographie kennen, aber sie besitzen, wie diese, ein regelmäßiges periodisches Gitter aus Atomen. Dies ist die Ursache für die Anisotropie vieler ihrer Eigenschaften. Die Kristallite bilden zusammen ein vielkristallines Aggregat. Die Eigenschaften eines solchen Stoffes hängen in erheblichem Maße davon ab, wie die anisotropen "Baugruppen" im Aggregat zusammengefügt sind. Dies wird durch die "Orientierungsstereologie" [1] beschrieben.
Die Grundgröße der Orientierungsstereologie ist die Mikrostrukturfunktion g(x). Sie gibt in jedem Punkt x = {x1, x2, x3} des Materials die dortige Orientierung g = {φ1, Φ, φ2} der Kristallachsen an. Bis vor kurzem gab es noch keine Messtechnik, um g(x) zu messen. Die klassische Texturmessung z.B. mit Röntgenbeugung ergibt nur den Volumenanteil aller Kristallite der Orientierung g an (kristallographische "Textur" [2, 3]), nicht aber deren räumliche Verteilung (Stereologie):
Der Hauptnachteil des traditionellen Ansatzes war das Fehlen einer direkten Verbindung zwischen der Untersuchung der Mikrostruktur und der Kristallographie. Dies bedeutet, dass, obwohl die gesamte durchschnittliche Orientierungsverteilung gemessen werden konnte, die Orientierung einzelner Kristalle nur in geringem Umfang und mit langwierigen Mitteln aus dieser Datenbank herausgezogen werden konnte. Daher war eine Fülle von Informationen über die räumlicheKomponente von Kornorientierungen, einschließlich der Grenzflächenbereiche, in denen sich Körner verbinden, nicht zugänglich. Das liegt an den Einschränkungen der klassischen mikroskopischen Methoden. Sie lassen zwar das Netzwerk der Korngrenzen erkennen und differenzieren eventuell unterschiedliche Phasen und Körner, wie sie in Gefügebildern dargestellt werden und die Grundlage für die quantitative Stereologie bilden [4, 5]. Sie geben aber normalerweise keine Auskunft über die Kristallorientierung. Man erhält nur die Koordinaten x1, x2, x3 der Korngrenzen, beschrieben durch derenFlächengleichung: F(x1, x2, x3) = 0 Stereologie (2). Die Orientierungsstereologie in Form der Mikrostrukturfunktion dagegen enthält beide Informationen gleichzeitig [1]: g = g(x1, x2, x3) Orientierungsstereologie (3). Volumentextur und Stereologie sind jeweils Projektionen der Orientierungsstereologie. Die Orientierungsstereologie enthält aber ungleich viel mehr Information als Volumentextur und konventionelle Stereologie zusammengenommen. Kennt man die Orientierungsstereologie, so kann man daraus Volumentextur und Stereologie, sowie viele andere Derivatfunktionen ableiten, aber nicht umgekehrt. Die Orientierungsstereologie Gl. (3) kann als zeitgemäße Erweiterung der klassischen Definitionen von Textur nach Gl. (1) und Stereologie Gl. (2), die durch die damaligen begrenzten Messmöglichkeiten bedingt waren, angesehen werden. 2. Wie misst man Orientierungsstereologie? Zur Messung der Mikrostrukturfunktion g(x) müssen sehr viele lokale
Kristallorientierungen meist in sehr kleinen Volumenelementen (ca. l µm) und möglichst schnell ermittelt werden, um auch dynamische Experimente verfolgen zu können. Dies wurde möglich durch die Weiterentwicklung der
Weitwinkel-Elektronenbeugung (Kikuchi-Diagramme) zu einer vollautomatischen,
computergesteuerten Technik (vgl. http://www.ebsd.info). Das Prinzip dieser Technik, die heute sowohl im
"Durchlicht" als auch im "Auflicht" zur Verfügung steht,
ist in Bild 1 erläutert:
Bei der Orientierungsmessung kann man auch verschiedene Phasen im Werkstoff anhand ihres Kristallgitters erkennen. Eine Zusatzeinrichtung – EDX – gestattet eine lokale chemische Analyse mit dem Elektronenmikroskop, ein unabhängiges Verfahren zur Verifikation der vorhandenen Phasen. Und schließlich kann man – insbesondere im Durchstrahlbetrieb – Versetzungsstrukturen sehen und analysieren. Die Kombination dieser drei mikroanalytischen Verfahren führt zu einer umfassenden quantitativen Beschreibung des Aggregatzustandes mittels der Allgemeinen Mikrostrukturfunktion oder Aggregatfunktion G(x):
Fazit: Ein ACOM-Gerät ist eines der universellsten Instrumente der Materialwissenschaften. 3. Einfluss auf die Werkstoffeigenschaften Die Richtungsabhängigkeit von Kristalleigenschaften hat drei wichtige Folgen
für die Werkstoffeigenschaften:
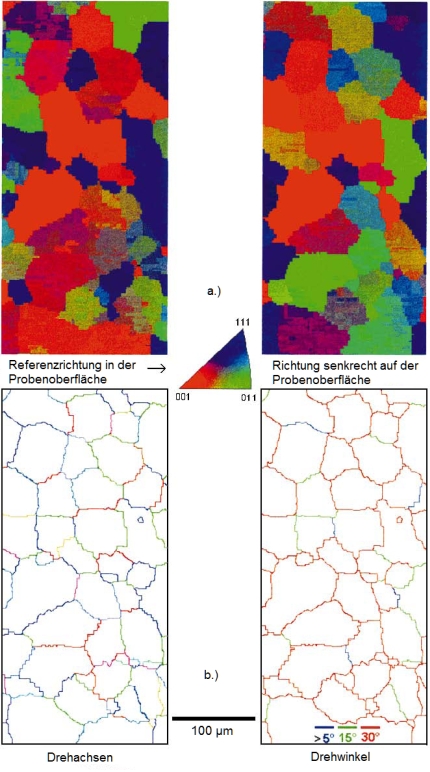
Die drei Effekte sind in Bild 3 erläutert. Alle drei hängen von der Orientierungsstereologie ab und sind durch die "Derivationsgrößen" Volumentextur und Stereologie allein nur unvollständig zu erfassen. Die Orientierungsstereologie, beschrieben durch die Mikrostrukturfunktion g(x), beeinflusst alle Stoffeigenschaften, die im Einkristall anisotrop sind (auch wenn der Werkstoff makroskopisch isotrop ist), Bild 4 rechts. Andererseits "entsteht" sie selbst durch alle anisotropen physikalischen Prozesse, die in der "Lebensgeschichte" des Stoffes abgelaufen sind, Bild 4 links. Das können technologische, geologische oder biologische Prozesse sein. Die Orientierungsstereologie und ihr Zusammenhang mit den Stoffeigenschaften ist daher von grundlegender Bedeutung für alle Stoffklassen (technologische, geologische, biologische), für alle Werkstoffe (neue High-Tech-Werkstoffe und Nanowerkstoffe gleichermaßen wie konventionelle) und für fast alle ihrer Eigenschaften. 4. Von der Mikrostrukturfunktion abgeleitete Funktionen (Derivationen) 4.1. Farbkodierte Darstellung der Orientierungsstereologie Wenn wir zwei von drei Parametern auswählen, die die Orientierung g(x) beschreiben, dann können diese mit einem Farbdreieck "farbcodiert" werden. Dies ist eine Methode [9] zur anschaulichen grafischen Darstellung einer zweidimensionalen Größe. 4.1.1. Kristallit- oder Korn-Stereologie Kornorientierungen g können durch zwei kristallographische Richtungen angegeben werden. In den Materialwissenschaften sind [hkl] und [uvw] gebräuchlich, das heißt eine Richtung parallel zur Probennormalen und eine Bezugsrichtung in der Probenoberfläche. Beide Richtungen können farbkodiert sein, wie in Bild 2 gezeigt. Die vollständige Darstellung von g(x) erfordert also zwei solche Projektionen, und es bedarf noch einiger "Gehirnarbeit", um sich die Orientierung g an einem Punkt x durch gleichzeitige Berücksichtigung der Farben der entsprechenden Punkte in beiden Bildern vorzustellen. Wenn Euler-Winkel, Miller Indizes oder die Rodrigues-Vektoren zur Farbcodierung verwendet werden, ist die Parametrisierung weniger intuitiv und mehrdeutig [10]. 4.1.2. Korngrenzen-Stereologie Eine Korngrenze ist durch die Rotation Δg gekennzeichnet, die die zwei Orientierungen g1 und g2 auf beiden Seiten der Grenze miteinander in Beziehung setzt. Diese Rotation kann beispielsweise durch drei Euler-Winkel {φ1, Φ, φ2} oder durch die Drehachse-Drehwinkel-Darstellung {r, ω} der Orientierungsdifferenz beschrieben werden:
Somit kann die Korngrenzen-Stereologie ebenfalls durch zwei graphische Darstellungen veranschaulicht werden, von denen eine eine Farbcodierung der kristallographischen Richtung der Rotationsachse r und die andere eine Kodierung in Grau oder einer Regenbogenfarbskala des (eindimensionalen) Rotationswinkels ω sein kann. Ein Beispiel ist in Bild 2b gezeigt. Die Angabe nur eines der Parameter, entweder der Drehachse oder des Drehwinkels, reicht nicht aus, um eine Korngrenze zu charakterisieren. Eine spezielle diskrete Version von Δg ist die Σ-Klassifikation von Korngrenzen nach dem Koinzidenzgitter-Modell. Dies ist jedoch nur eine grobe Annäherung an die exakte Fehlorientierung. 4.2. Missorientierungs-Verteilungsfunktion Die Missorientierungs-Verteilungsfunktion (MODF) gibt den Flächenanteil von Korngrenzen an, die eine bestimmte Fehlorientierung Δg haben:
Die MODF ist eine dreidimensionale Verteilungsfunktion, die auf ähnliche Weise, z.B. durch Euler-Winkel, wie die ODF in der klassischen Textur, Gleichung 1, dargestellt werden kann. Sie berücksichtigt ebenfalls nicht die geometrische Lage der einzelnen Korngrenzen im Raum. 4.3. Texturfelder
Das klassische Konzept der Textur, Gleichung 1, kann auf kleinere (aber immer noch polykristalline) Teilvolumina der Probe angewendet werden, wie es in Bild 5 dargestellt ist. Wenn diese lokale Textur als eine Funktion der Position X der Volumenelemente der Probe betrachtet wird, wird dies ein Texturfeld genannt:
Da sowohl g als auch X dreidimensionale Größen sind, ist ein Texturfeld eine sechsdimensionale Funktion, die in gleicher Weise wie die Orientierungsstereologie an ihrer "Hochdimensionalität" krankt. Daher benötigt die Texturfeldfunktion eine weitere Datenreduktion für ihre anschauliche Darstellung. 4.4. Korngrößenspezifische Textur Das klassische Konzept der Textur, d.h. unter Berücksichtigung des Volumenanteils von Körnern mit einer bestimmten Orientierung g, kann selektiv auf Körner (in der gesamten Probe) mit einer gewählten spezifischen Korngröße ρ klassifiziert werden:
wobei Vρ der Volumenanteil von Körnern der Größe ρ ist. Diese Funktion spielt eine wichtige Rolle bei Rekristallisations-, Kornwachstums- oder Sinterprozessen. Die korngrößenspezifische Textur kann nicht mit einer eigenen Technik gemessen werden. Daher ist sie eine echte Ableitung von g(x). 4.5. Eigenschafts-Stereologie (Mikroskala) Die lokalen physikalischen Eigenschaften P des Materials am Ort x hängen in der Regel von der Orientierung g des Kristallgitters an dieser Stelle ab. Wenn man die Orientierungsabhängigkeit einer Kristalleigenschaft P(g) einerseits und die lokale Orientierung g(x) andererseits kennt, können diese beiden Beziehungen kombiniert werden. Man erhält somit die lokale Eigenschaft am Ort x P(x) = P(g(x)) Eigenschafts-Stereologie (9) Sie kann direkt als Funktion von x aufgetragen werden, wenn die Mikrostrukturfunktion g(x) gemessen wurde. Dieser Ansatz ist besonders praktisch, wenn P eine eindimensionale Eigenschaft ist, wie beispielsweise der Elastizitätsmodul (Elastizität) oder der Taylor-Faktor (Plastizität). Die Funktion P(x) ist eine echte Ableitung von g(x), da in den meisten Fällen direkte Messtechniken für P(x) nicht existieren, zumindest nicht mit der hohen räumlichen Auflösung der aktuellen Einzelorientierungs-Messverfahren. 4.6. Eigenschaftsfelder (Mesoskala) Lokale physikalische Eigenschaften können auch in polykristallinen Volumenelementen an der Stelle X betrachtet werden. Sie sind Mittelwerte der Kristalleigenschaften P(x). Die Eigenschaftswerte im Volumenelement hängen sowohl von der lokalen Textur f(g, X) als auch von der Stereologie innerhalb dieses Volumenelements ab. Dennoch ist die erste Näherung, die nur von der (lokalen) Textur f(g, X) ausgeht, oft ein ziemlich brauchbarer Wert. Daher kann es zweckmäßig sein, die beiden Beziehungen P(g) und f(g, X) zu kombinieren. Man erhält so das Eigenschaftsfeld:
Dies ist eine echte Ableitung der Texturfeld-Funktion f(g, X), da direkte Messtechniken für P(X) normalerweise nicht existieren, zumindest nicht mit der gleichen räumlichen Auflösung wie für f(g, X).
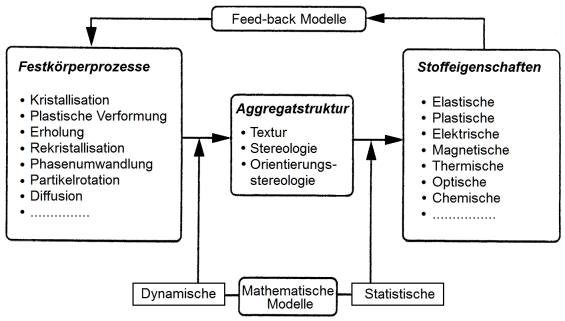
5. Mathematische Modelle Es ist ein wichtiges Ziel der Werkstoffwissenschaften, die beiden
Zusammenhänge von Bild 4 zunächst einzeln in mathematischen Modellen zu
erfassen. Um technologische Prozesse modellieren zu können, ist
dann meistens noch eine "Rückkopplung" zwischen beiden zu
berücksichtigen, wie sie ebenfalls in Bild 4 angegeben ist. Bekanntestes
Beispiel hierfür ist die Werkstoffumformung z.B. beim Tiefziehen: Die
Werkstoffeigenschaft beeinflusst den Ziehvorgang, dieser wiederum verändert die
Werkstoffeigenschaften, und das setzt sich so fort bis zum Endumformgrad.
Mathematische Modelle, Bild 4, müssen die vollständige Orientierungs-Stereologie
berücksichtigen. Modelle auf der Basis der Volumentextur oder Stereologie
allein reichen dazu nicht aus. Dies ist zwar keine neue Erkenntnis, aber
solange man die Orientierungsstereologie nicht messen konnte, standen solche
Modelle auf unsicherem Boden. Außerdem erfordern sie einen größeren
rechentechnischen Aufwand als einfachere Modelle. 6. Folgerungen Die Orientierungsstereologie ist die grundlegende Strukturgröße des vielkristallinen Zustandes der festen Materie. Sie ist daher das Bindeglied zwischen Kristallographie und Festkörperphysik einerseits und Werkstofftechnologie andererseits. Die wechselseitigen Beziehungen zwischen diesen Gebieten sind in Bild 6 gezeigt:
Neben den oben explizit aufgeführten Ableitungsfunktionen können viele andere definiert werden (und wurden verwendet). Jede dieser Funktionen betont einen bestimmten Aspekt, der in der Mikrostrukturfunktion g(x) enthalten ist, wobei jedoch gleichzeitig andere Aspekte vernachlässigt werden. Dies trägt unserer begrenzten menschlichen Vorstellungskraft Rechnung. Mathematische Modelle, die auf g(x) basieren, können jedoch die gesamte in g(x) enthaltene Information quantitativ verarbeiten. Daher eröffnen die aktuellen Verfahren zur Messung der Orientierungsstereologie g(x) und die Verfügbarkeit von darauf basierenden mathematischen Modellen einen neuen Bereich der Materialeigenschaftsmodellierung. Literatur
| ||||||||||||||||||||||||||||||||||||||

 Volumentextur ODF (1).
Volumentextur ODF (1).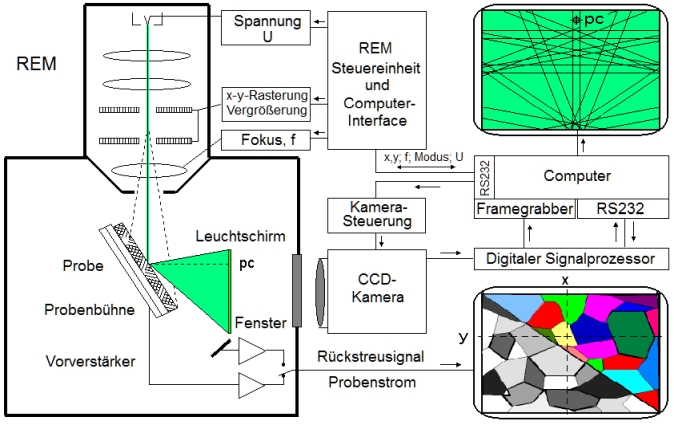
 Aggregatfunktion (4)
Aggregatfunktion (4)
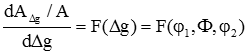 MODF (6).
MODF (6).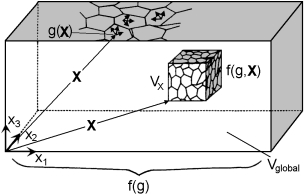
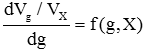 Texturfeld (7)
Texturfeld (7)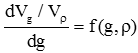 Textur klassifizert nach Korngröße (8)
Textur klassifizert nach Korngröße (8)